왜 $e^{iπ}$ 가 $-1$일까 ━ 오일러 등식
세상에서 가장 아름다운 수식, 오일러 등식에 대하여.
Inspired by "유튜브 - 세상에서 가장 아름다운 수식을 이해해보자 (문과용) by DMT PARK"
블록버스터 급의 뛰어난 퀄리티의 영화, 광활하게 펼쳐진 대자연을 보다보면 우리는 경이로움과 아름다움, 그리고 감탄을 금치 못한다. 이 외에도 이 세상엔 충분히 감탄할 만한 가치가 있는 것들로 가득하다. 하지만, '수(數)' 라는 기본적이고 추상적인 이론을 바탕으로 이루어지는 수학에도 과연 아름다움이 존재할 수 있을까?
중/고등학교 시절에 배운 수학에 대해 생각해보자. 국어와 영어 모두 어렵지만, 수학이 보통 중/고등학생들의 최종 보스라고 여겨진다. "국포자" 또는 "영포자"는 들어본 적이 없어도 "수포자" 는 살면서 한 번 쯤은 들어본 적이 있을 것이다. 이런 대한민국 교육과정의 최종 보스로 여겨지는 수학에서 "아름다움"을 찾아 헤멘다는 것이 모순으로 느껴지는 것은 사실이다. 그러다가 흥미로운 설문조사를 발견하게 되었다.
1988년, 수학 저널 < Mathematical Intelligencer > 에서 흥미로운 설문조사를 하게 되었는데, 24개의 저명한 수학 공식을 나열하고 독자들에게 무엇이 가장 아름다운 공식인지 설문하였다. 이 설문조사에서 1등을 한 수학 공식이 오늘 이야기할 오일러 항등식 이다.
오일러 항등식은 무엇일까?
오일러 항등식(이하 "오일러 등식"이라 함.) 은 위대한 수학자 레온하르트 오일러의 이름이 붙은 공식이다. 오일러 등식은 다음과 같다.
$$e^{i\pi} + 1 = 0$$
아주 극단적으로 단순한 등식이라 할 수 있는데, 왜 세상에서 가장 아름다운 등식이라고 하는 것이냐면, 수학에서 가장 자주 쓰이는 수인 0, 1, 자연로그의 밑인 $e$, 허수 $i$, 원주율 $\pi$ 가 모두 모여 하나의 등식을 이룬다는 것 때문이다. 뿐만 아니라 수학의 기초인 사칙연산과 지수, 등호가 모두 쓰였다는 점에서 더욱이 의미있다.
오일러 등식의 기초
위키피디아 https://ko.wikipedia.org/wiki/오일러_공식 참조.
오일러 "등식"의 기본은 오일러의 "공식"에서 나온 것이다. 오일러의 공식은 다음과 같다.
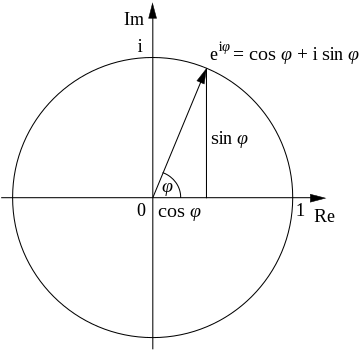
$$e^{ix} = \cos x + i\sin x$$
여기서 $e$는 자연로그의 밑이고, $i$는 허수의 단위( $i^2 = -1$ ), $\sin$과 $\cos$는 차례대로 삼각함수의 사인, 코사인 함수이다. 오일러 등식은 오일러의 공식에 $x=\pi$ 를 대입한 특수한 경우이다. $\cos\pi$는 $-1$이고, $i\sin\pi$는 $0$이므로, $e^{i\pi} + 1 = 0$ 라는 식이 나오는 것이다.
$e^{i\pi}$? $e$를 $i\pi$번 곱한건가?
이 등식을 보자마자 가장 먼저 든 생각은 "이게 계산이 가능한가" 에 대한 질문이었다. 보통 지수에는 자연수, 고등학교 2학년 과정의 수I, 지수 단원에서 지수의 개념을 확장하긴 하지만, 지수에 무리수인 $\pi$, 더 나아가 복소수에서 배우는 허수단위 $i$가 들어가는 것은 여태 수학을 공부하면서 접해본 적이 없었다. 이 당시에 나는 수1을 갓 마친 예비 고2였다. 아무튼 본론으로 돌아가, $e^{i\pi}$라는 개념을 알기 위해 우선 우리는 자연로그의 밑인 $e$ 라는 것에 대해 알아야 한다.
자연로그의 밑, $e$
$e$를 흔히 자연상수라고 부르기도 하는데, 공식 명칭은 "자연로그의 밑" 이므로, 이 글에서도 자연로그의 밑이라고 표현하겠다. 자연로그의 밑 $e$는 무리수이면서 그 동시에 초월수 이다. $e$를 정의하는 가장 일반적인 방법은 함수의 극한을 이용한 정의이다. 전문용어로 "야코프 베르누이의 계산법"이라고도 한다.
$$e = \lim_{x\to \infty}{\left(1+\frac{1}{x} \right)^{x}}$$
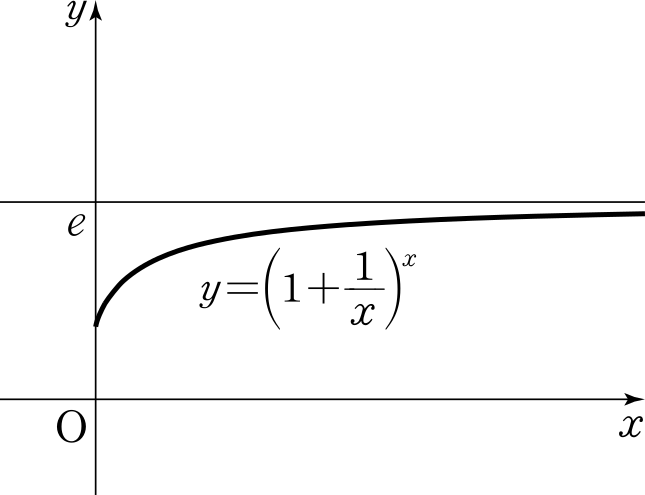
$N$ 을 셀 수 없이 아주 큰 수 라고 정의하고, 극한 기호를 없애 단순히 자연로그의 밑 $e$를
$$e = {\left(1+\frac{1}{N} \right)^{N}}$$
라고 해보자. $e$를 제곱한 $e^2$는 다음과 같이 나타낼 수 있다.
세상에서 가장 아름다운 수식을 이해해보자 (문과용) 에서 인용함.
$$e^2 = {\left(1+\frac{1}{N} \right)^{2N}}={\left(1+\frac{2}{N} + \frac{1}{N^2} \right)^{N}}$$
여기에서 $\frac{1}{N^2}$은 무시하고 (너무 작은 수이기 때문에 이를 무시한다 해도, 무시하지 않았을 때의 수식과 같은 값으로 수렴하기 때문이다.), $e^2$을 다음과 같이 재정의 해보자.
$$e^2 = {\left(1+\frac{2}{N} \right)^{N}}$$
같은 방법으로 $e^3$, $e^4$도 정의해보자.
$\displaystyle e = {\left(1+\frac{1}{N} \right)^{N}}$
$\displaystyle e^2 = {\left(1+\frac{2}{N} \right)^{N}}$
$\displaystyle e^3 = {\left(1+\frac{3}{N}+\frac{3}{N^2}+\frac{1}{N^3} \right)^{N}}$
$\displaystyle e^4 = {\left(1+\frac{4}{N}+\frac{6}{N^2}+\frac{4}{N^3}+\frac{1}{N^4} \right)^{N}}$
$\frac{1}{N^2}$을 무시한 것과 같이 계산식을 줄여보면,
$\displaystyle e = {\left(1+\frac{1}{N} \right)^{N}}$
$\displaystyle e^2 = {\left(1+\frac{2}{N} \right)^{N}}$
$\displaystyle e^3 = {\left(1+\frac{3}{N} \right)^{N}}$
$\displaystyle e^4 = {\left(1+\frac{4}{N}\right)^{N}}$
이렇게 나타낼 수 있다. 자세히 보면 규칙성이 존재하는데, $e$의 지수 자리에 들어가는 수가 분모가 N인 분수의 분자로 들어가는 것을 볼 수 있다. 그래서 $e^m$을 다음과 같이 정의할 수 있다.
$$e^m = {\left(1+\frac{m}{N}\right)^{N}}$$
그렇기 때문에 $e^{i\pi}$를 $e^{i\pi} = {\left(1+\frac{i\pi}{N}\right)^{N}}$ 로 나타낼 수 있는 것이다.
마무리하며
DMT PARK 님의 영상을 보고 영감을 받아 이렇게 글을 써보았고, 자연로그와 오일러 공식에 대해서 자세히 공부해볼 수 있는 기회가 되었다. 앞으로도 이러한 수학 관련 포스팅을 올려볼 생각이다.
