정형 데이터 분류를 이용한 DDoS 공격 예측 모델 제작
나이브 베이즈 분류를 중심으로
초록
본 보고서는 정형 데이터 분석법의 기본적인 개념을 소개하고 나이브 베이즈 분류(Naïve Bayes Classification) 알고리즘을 이용하여 데이터셋을 분석, 예측할 수 있도록 모델을 학습하고, 성능을 비교· 분석·개선하였다.
본 보고서에서는 DDoS(Distributed Denial of Service) 공격 로그 데이터를 이용해 네트워크 요청이 정상/비정상인지 분류하고 예측하는 모델을 학습시키는 연구를 진행하였다. 본 연구를 통해 첫 시도로 학습된 모델은 DDoS 공격 진위 여부를 약 49%의 정확도로 분류하였다. 첫 시도의 분류 결과를 토대로 모델의 문제점을 분석하고 개선하였으며, 그 결과로 정확도를 76%까지 개선할 수 있었다.
주제어: 확률과 통계, 머신 러닝, 데이터 마이닝, 컴퓨터공학
그림 목차
Fig. 1. 무어의 법칙(Moore’s Law)의 그래프
Fig. 2. 과소적합과 정적합, 과대적합의 산점도 비교
Fig. 3. DDoS 데이터셋의 일부
Fig. 4. BENIGN과 DDoS의 비율
Fig. 5. 특성에 대한 상관관계도
Fig. 6 Confusion Matrix #1
Fig. 7. train_size에 대한 accuracy의 변화 그래프
Fig. 8. Confusion Matrix #2
표 목차
Table. 1. Confusion Matrix #1 (train_size=0.7)
Table. 2. Predict Score #1 (train_size=0.7)
Table. 3. 혼동행렬의 구조
Table. 4. 혼동행렬 지표의 계산법
Table. 5. train_size에 대한 accuracy의 변화 데이터
Table. 6. Confusion Matrix #2 (train_size=0.18)
Table. 7. Predict Score #2 (train_size=0.18)
기호 설명
기호
i.e. id est, 즉, 다시 말하여
e.g. exempli gratia, 예를 들어
etc. et cetera, 기타, ~등
fig. figure, 그림
두문자어
NBC Naïve Bayes Classification, 나이브 베이즈 분류
DDoS Distributed Denial of Service, 분산 서비스 거부 공격
GNB Gaussian Naïve Bayes, 가우시안 나이브 베이즈
1. 서론
1.1 연구 배경과 목적
인간사(史)에 있어 인쇄술의 발전은 정보의 혁명이었다고 해도 과언이 아닐 것이다. 15세기 중반에 유럽에서부터 발달한 인쇄술은 책 하나를 필사하는 데 수 개월이 걸리던 고된 작업을 단 며칠 만에 끝날 수 있도록 하였고, 이 이후로 인간은 책을 매개체로 지식을 빠르게 생산·전달·습득할 수 있게 되었다. 하지만 그 당시의 학자들은 인쇄술의 발달로 인한 방대한 책 생산에 대해 부정적 견해를 제시하기도 하였다. 독일의 수학자 라이프니츠는 “책이 쏟아져나오는 양이 끔찍할 정도로 늘어나면 결국 야만의 시대로 되돌아가는 결과가 될 것”이라 우려하는 입장을 보이기도 했다.
현재 우리가 생산하는 정보의 기조는 무어의 법칙(Moore’s Law)과 상당히 유사하다. 무어의 법칙은 “마이크로칩 기술의 발전 속도에 관한 법칙으로 마이크로칩에 저장할 수 있는 데이터 분량이 18-24개월 마다 두 배씩 증가한다는 법칙” (기획재정부 시사경제용어사전, 2020) 이다. 1965년 발표된 무어의 법칙은 “인터넷은 적은 노력으로도커다란 결과를 얻을 수 있다”는 메트칼프의 법칙, “조직은계속적으로 거래비용이 적게 드는 쪽으로 변화한다”는 가치사슬의 법칙과 함께 인터넷 경제의 3원칙으로 불린다 (기획재정부 시사경제용어사전, 2020). 기술이 발전함에 따라 반도체 집적 속도가 무어의 법칙을 따라가지 못해 결국 이 법칙은 무용지물이 되었다. 하지만 정보 생산의 측면에서 무어의 법칙을 바라본다면 아직 유효하다고 볼 수 있다. 오히려 절대적인 생산 증가량만 고려한다면 무어의 법칙을 뛰어넘는다고 말할 수 있다.
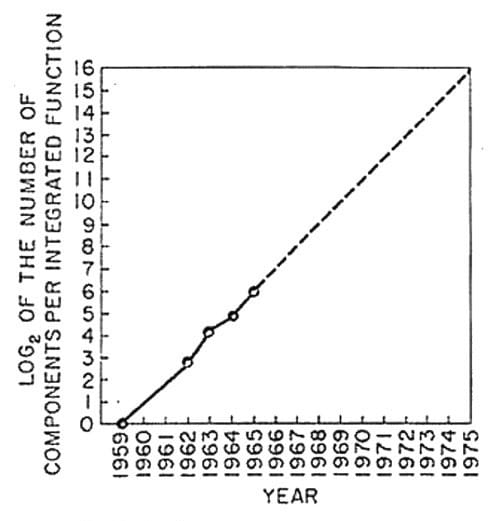
현재 우리가 생산하는 정보는 이미 우리의 수용 범위를 아득히 뛰어넘었다. 이는 정보와 매체 기술의 발달도 원인이지만, 가장 큰 원인은 정보의 종류, 전달 방식이 획기적으로 발전한 것에 있다. 우리는 전 지구적으로 퍼져있는 인터넷망으로 형성된 월드 와이드 웹(World Wide Web)을 통해 영상을 시청하거나 필요한 자료를 바로 검색할 수 있게 되었다. 前 구글 최고경영자 Eric Schmidt는 2010년에 개최된 한 컨퍼런스에서 “인류 문명이 출현한 시점부터 2003년까지 만들어낸 정보는 5엑사바이트* 수준이고 오늘날에는 단 이틀이면 인류 문명 이후 축적된 만큼의 정보를 생산한다”고 발언했다. 이를 반증하듯 현재의 우리는 데이터를 꾸준하게, 그리고 아주 많이 생산하고 있다. 1분동안 전 세계에선 약 2억개의 이메일이 오가고, 세계 최대 규모의 검색 엔진인 구글(Google)에서만 1분 당 약 410만 번의 검색이 이루어진다. 전 세계에서 1분동안 만들어지는 데이터를 수치로 본다면 약 1,400TB(i.e. 1,400,000GB)이다.
앞선 설명처럼 현재를 살아가는 우리는 막대한 양의 데이터를 마주한다. 그러나 정작 이런 데이터들을 잘 활용하고 있다고는 보기 어렵다. 우리가 생산하는 대부분의 데이터는 과도한 잉여로써 남아 분석·활용되지 못하고 폐기되거나 방치된다. 이런 과도한 데이터의 잉여는 앞선 라이프니츠의 말처럼 인간이 야만의 시대로 되돌아가도록 이끌지는 않을 것이다. 그러나 이는 정보화 시대에서 대단한 손실이라고 할 수 있다. 우리는 우리가 창출한 데이터를 보다 잘 이해하고 유연하게 활용할 줄 알아야 하는 것이다.
데이터를 다루는 능력은 컴퓨터공학 전공을 희망하는 내게 있어 무엇보다 중요하지만 학기 중에 이것을 배우기엔 시간이 턱없이 부족했다. 내가 자유로이 원하는 공부를 할 수 있는 소중한 방학을 이용해서 데이터의 분류와 처리에 대해 배우기로 했고, 일련의 과정을 통해 축적된 데이터를 통해 제 3의 데이터가 유입되었을 때 이를 분류하고 예측할 수 있는 모델도 만들어보는 연구를 진행하기로 하였다. 이 보고서는 데이터 전처리 과정을 통해 변수와 변수 사이의 상관관계와 인과관계를 살펴보고, 데이터 분류기 알고리즘을 이용해 데이터를 기준에 맞게 분류, 예측하는 원리와 과정을 삼펴봄으로써 데이터에 대한 더욱 폭 넓은 이해를 얻고자 했다.
2. 본론
2.1 분류 알고리즘
기계 학습(Machine Learning)은 크게 ‘지도 학습’(Supervised Learning)과 ‘비지도 학습’(Unsupervised Learning)으로 나눌 수 있다. ‘지도 학습’은 기계에게 문제와 정답을 모두 제공하여 학습시키는 방법으로, 주로 데이터를 예측하거나 분류할 때 주로 사용한다. 반면 ‘비지도 학습’(Unsupervised Learning)은 기계에게 문제만 제공하여 학습시키는 방법으로, 주로 데이터간의 연관성을 찾아내거나 데이터들을 군집화(Clustering)할 때 사용한다. 이 보고서에선 ‘지도 학습’을 주로 다룬다.
지도 학습을 위해서 원본 데이터를 크게 세 종류로 분할한다. ‘학습 데이터’(Training Data)는 모델을 학습하는데 사용하는 데이터셋(Data Set, 데이터 집합)으로, 학습 데이터가 많으면 많을수록 모델의 성능(i.e. 예측 정확도)이 증가한다. ‘테스트 데이터’(Test Data)는 학습 데이터를 통해 학습된 모델의 성능을 평가하는데 사용되는 데이터셋이다. 테스트 데이터는 학습 데이터에 포함되지 않은 독립적인 데이터여야 한다는 조건이 있다. 마지막으로 ‘검증 데이터’(Validation Data)는 학습 과정에서 학습을 중단할 시점을 결정하기 위해 사용하는 데이터셋이다. 검증 데이터는 학습에 사용할 학습 데이터에 포함되어 있으나 학습에 직접 이용되진 않는다. 대신 검증 데이터는 학습된 모델을 검증하기 위해 사용한다. 지도 학습에서 학습 데이터는 보통 전체 데이터의 70%~80%를, 모델의 검증에 필요한 테스트 데이터와 검증 데이터는 전체 데이터의 20%~30%를 차지한다.
한편, 모델을 학습시킬 때 절대적인 정확도만 중시하여 학습할 경우 과대적합(Overfitting)이 발생할 수 있다. 과대적합이란 학습 데이터에 대해 지나치게 잘 학습된 상태를 의미한다. 과대적합이 일어나게 되면 학습 데이터 이외의 데이터, 즉 테스트 데이터를 제대로 처리할 수 없다. 이러한 과대적합은 학습에 규제를 적용함으로써 해결할 수 있다. 반면 정확도를 너무 무시할 경우 이는 과소적합(Underfitting)을 일으킬 수 있다. 과소적합이란 학습 데이터에 대해 지나치게 덜 학습된 상태를 의미한다. 과소적합된 모델은 모델이 너무 단순하여 테스트 데이터를 제대로 처리하지 못한다. 분류 모델을 만들 때에는 모델이 과대적합과 과소적합을 이루지 않고 정적합(Good Fitting)을 이루도록 여러 요인을 고려하여 학습시켜야 한다.
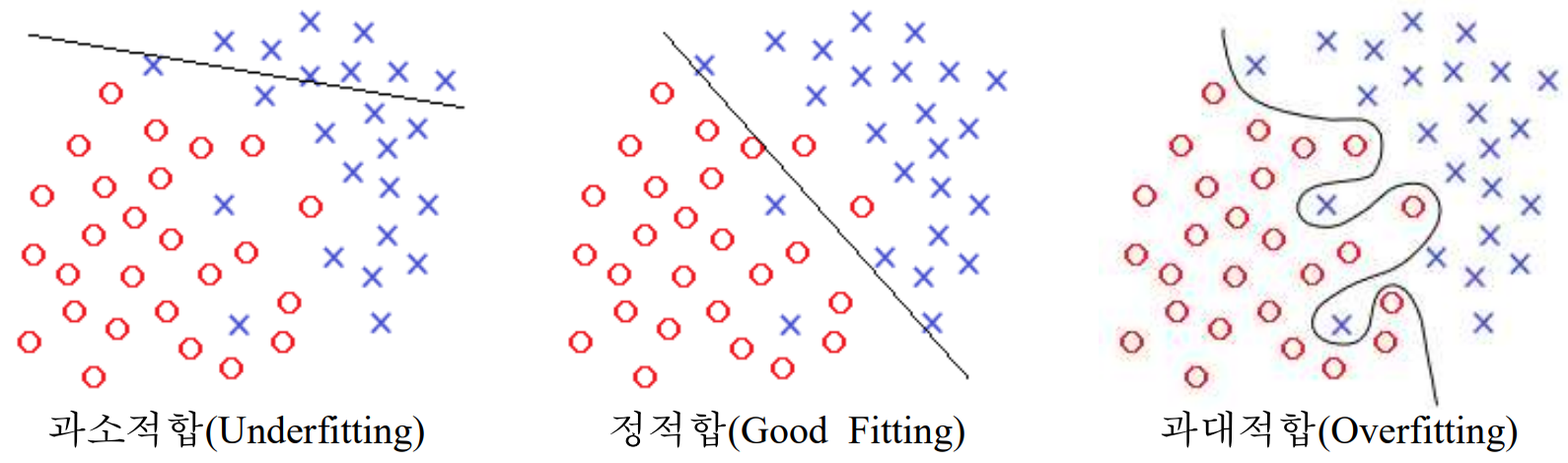
분류 알고리즘의 종류로 선형회귀(Linear Regression), 로지스틱 회귀(Logistic Regression), 나이브 베이즈 분류(Naïve Bayes Classification) 등 여러 가지가 있다. 이 보고서에선 나이브 베이즈 분류(NBC)를 사용한다.
2.2 나이브 베이즈
2.2.1 베이즈 정리(Bayes Theorem)
NBC를 이해하려면 베이즈 정리에 대한 사전 지식이 필요하다. 베이즈 정리는 두 확률 변수의 사전 확률과 사후 확률 사이의 관계를 나타내는 정리로, 사전 확률과 가능도를 데이터에 적용하여 사후 확률을 확인하는 조건부 확률이다. $P(B)>0$이라고 할 때 베이즈 정리는 다음과 같다.
$$P(A|B)=\frac{P(B|A)P(A)}{P(B)}$$
위 수식에서 $P(A|B)$는 의 사후확률(Posterior Probability), $P(B|A)$는 $B$의 조건부 확률, $P(A)$, $P(B)$는 각각 $A$와 $B$의 사전확률(Prior Probability)이다. 즉, 사전확률을 통해 사후확률을 예측하는 것이다.

2.2.2 나이브 베이즈 분류
NBC는 베이즈 정리를 이용한 확률 기반 지도 학습 분류 알고리즘으로, 부류(Class) 결정 지식을 조건부 확률로 결정한다. 베이즈 정리를 이용해 주어진 데이터가 특정 부류에 속할 확률을 계산하고 가장 높은 확률을 가진 클래스를 선택한다. 이때, 모든 특성(Feature)은 상호독립적(Mutually Independent)이라고 가정한다.
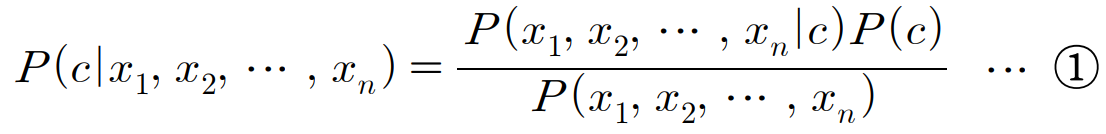
위 식에서 $P(c|x_1, x_2, ..., x_n)$는 속성값에 대한 부류의 조건부 확률, $c$는 부류, $x_i$는 속성값을 의미한다. 또한 나이브 베이즈 분류에서는 가능도(Likelihood)의 조건부 독립(Conditional Independence)도 가정한다.
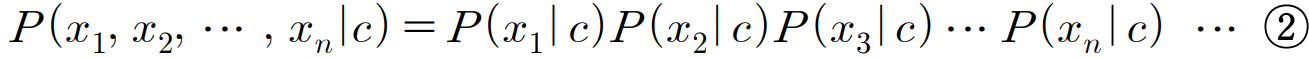
나이브 베이즈 분류는 간단하고 빠르며 효율적이고 특히 잡음과 누락 데이터 처리에 탁월하다. 예측을 위한 추정 확률을 쉽게 얻을 수 있다는 장점이 있지만 특징이 독립이라는 가정이 잘못되는 경우가 많다는 단점도 있다.
나이브 베이즈 분류는 다시 가우시안 나이브 베이즈(Gaussian Naïve Bayes, GNB)와 다항분포 나이브 베이즈(Multinomial Naïve Bayes), 베르누이 나이브 베이즈(Bernoulli Naïve Bayes)로 나뉜다. 이 보고서는 가우시안 나이브 베이즈에 대해 다룬다.
2.2.3 가우시안 나이브 베이즈
GNB를 이용해 연속적인 값을 지닌 데이터를 처리할 때에는 각 부류의 연속적인 값들이 가우스 분포를 따른다고 가정한다. e.g. 학습 데이터가 연속 속성 $x$를 포함한다고 가정하면, 부류에 따라 데이터를 나눈 뒤 각 부류에서 $x$의 평균과 분산을 계산한다. 부류 $c$와 연관된 $x$값의 평균을 $\mu_c$라 하고, 분산을 $\sigma_c^2$라 하면, 주어진 부류의 값들의 확률 분포가 매개변수화되어 정규분포식을 통해 계산될 수 있다.(Wikipedia, 2022)
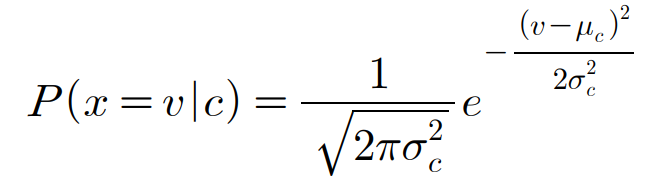
여기서 $e$는 자연로그의 밑이다. ($e=2.718281...$)
2.2.4 나이브 베이즈 분류 예시
아래 예시를 통해 나이브 베이즈 분류가 어떻게 이루어지는지 볼 수 있다.
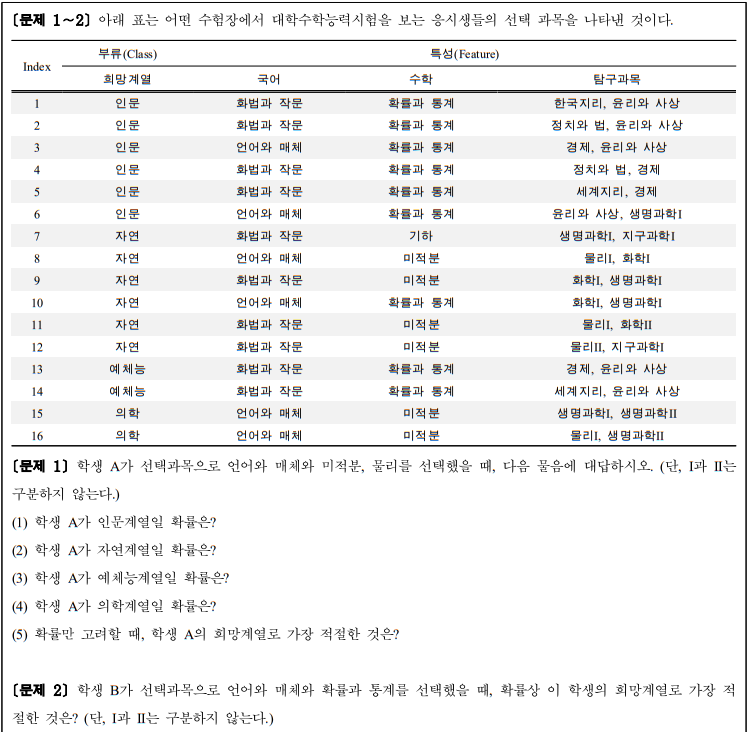


한편, 2.2.2에서 나이브 베이즈 분류의 단점으로 “특징이 독립이라는 가정이 잘못되는 경우가 많다”고 하였다.(p.4) 이 가정이 잘못된 경우, 1을 초과한 확률이 나타나는 모순이 생길 수 있다. 이런 단점 또한 이 예시를 통해 확인할 수 있다.
만일 화법과 작문과 미적분, 생명과학(I, II 구분 없음)을 선택한 수험생의 희망계열이 자연계열일 확률을 물어봤을 경우, 앞선 풀이과정(pp.6-7)을 통해 구하면 그 과정은 다음과 같다.

위 계산에 따르면, 화법과 작문과 미적분, 생명과학(I, II 구분 없음)을 선택한 수험생의 희망계열이 자연계열일 확률은 1.333...이 된다. 이는 확률의 성질에 위배된다. 이런 경우가 바로 “특징이 독립이라는 가정이 잘못되는 경우”인 것이다.
2.3 연구 과정
연구 환경으로 Python 3.10.6 환경에서 Scikit-learn 라이브러리를 사용하였다. 구동 환경은 32GB RAM, Intel(R) Core(TM) i5-8500 CPU @ 3.00GHz와 GPU는 NVidia GeForce RTX 3050을 사용하였다. 데이터셋은 Canadian Insitute for Cybersecurity(CIC)에서 제공한 CIC-DDoS2019 데이터셋을 이용한다.
2.3.1 데이터셋
DDoS 데이터셋은 Canadian Insitute for Cybersecurity(CIC)에서 제공한 CIC-DDoS2019 데이터셋을 사용한다. 이 데이터셋은 캐나다사이버보안대학교가 2017년 겪은 실제 DDoS 공격의 데이터셋으로, 2일 동안의 DDoS 공격 로그가 담겨있다. 85개의 열(Column)과 1048576개의 행(Row)으로 이루어진 약 21MB 용량의 데이터셋이다. 이 데이터셋은 서버와 클라이언트 간에 오간 패킷의 최대·최소·평균·표준편차, 트래픽의 양, 접속 아이피, 연결 시간, DDoS 여부 등을 포함하고 있다.
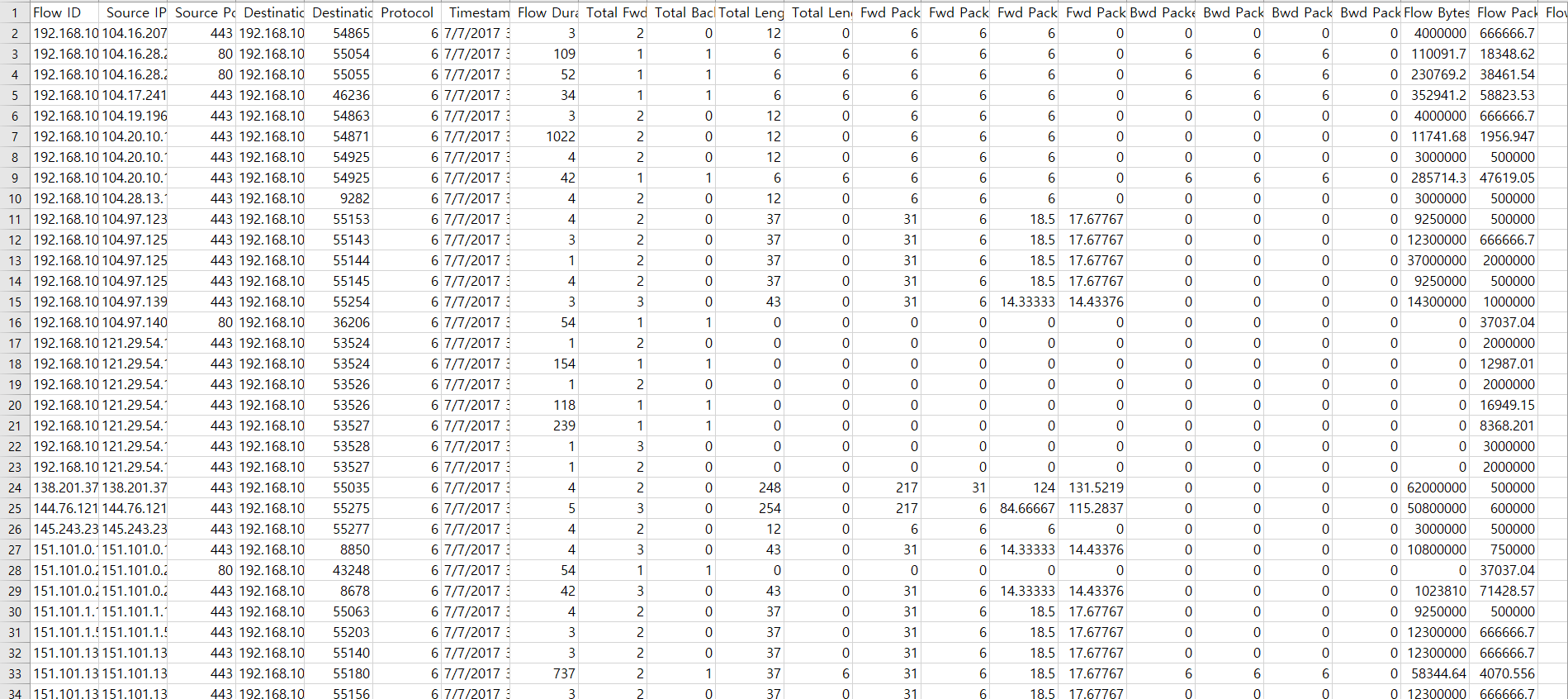
2.3.2 코드 작성
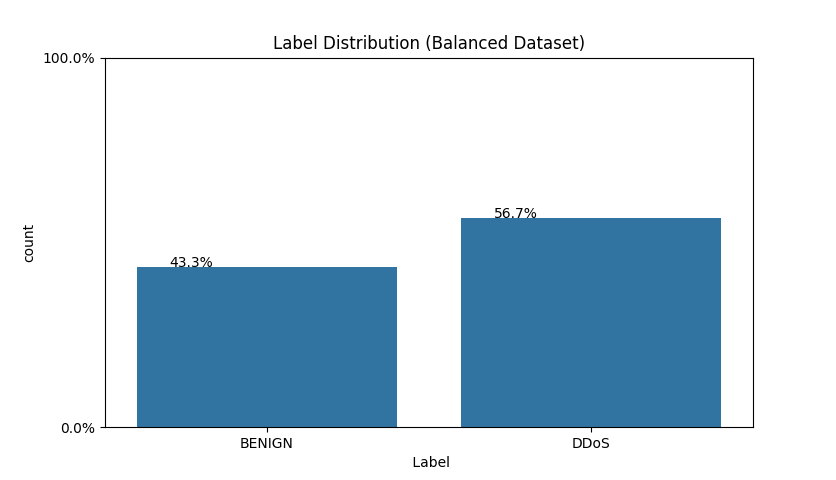
DDoS 데이터셋을 파이썬 코드로 불러온 후 BENIGN과 DDoS의 비율을 확인한다. Fig. 4
from sklearn import datasets
from sklearn.Naïve_bayes import GaussianNB
import numpy as np
import pandas as pd
from imblearn.over_sampling import SMOTE
from sklearn.metrics import confusion_matrix
from sklearn.model_selection import train_test_split
# module import endline #
data=pd.read_csv('./dataset.csv',chunksize=100000,index_col=0) # import dataset(csv)
df = pd.concat(data)
print ("Balanced Dataset shape: ")
print(df.shape)
total = len(df)*1.
ax=sns.countplot(x=" Label", data=df)
for p in ax.patches:
ax.annotate('{:.1f}%'.format(100*p.get_height()/total),(p.get_x()+0.1,p.get_height()+5))
ax.yaxis.set_ticks(np.linspace(0, total, 2))
ax.set_yticklabels(map('{:.1f}%'.format, 100*ax.yaxis.get_majorticklocs()/total))
plt.title('Label Distribution (Balanced Dataset)')
plt.show()
불러온 데이터 중 target과 feature를 정한다. target은 정답인 Label을 사용하고 feature은 timestamp를 제외한 다른 모든 데이터를 사용한다. 그리고 train_test_split을 사용해 Training Data와 Test Data로 분할한다. Training Data는 0.7(70%), Test Data는 0.3(30%)로 설정한다.
x=df[[' Flow Duration',' Total Fwd Packets', ' Total Backward Packets','Total Length of Fwd Packets', ' Total Length of Bwd Packets',' Fwd Packet Length Max', ' Fwd Packet Length Min',' Fwd Packet Length Mean', ' Fwd Packet Length Std','Bwd Packet Length Max', ' Bwd Packet Length Min',' Bwd Packet Length Mean', ' Bwd Packet Length Std','FIN Flag Count', ' SYN Flag Count', ' RST Flag Count', 'Idle Mean', ' Idle Std',' Idle Max', ' Idle Min']]
y=df[' Label']
y=data[' Label']
X_train, X_test, y_train, y_test = train_test_split(x, y, train_size=0.7, shuffle=False, random_state=1004)
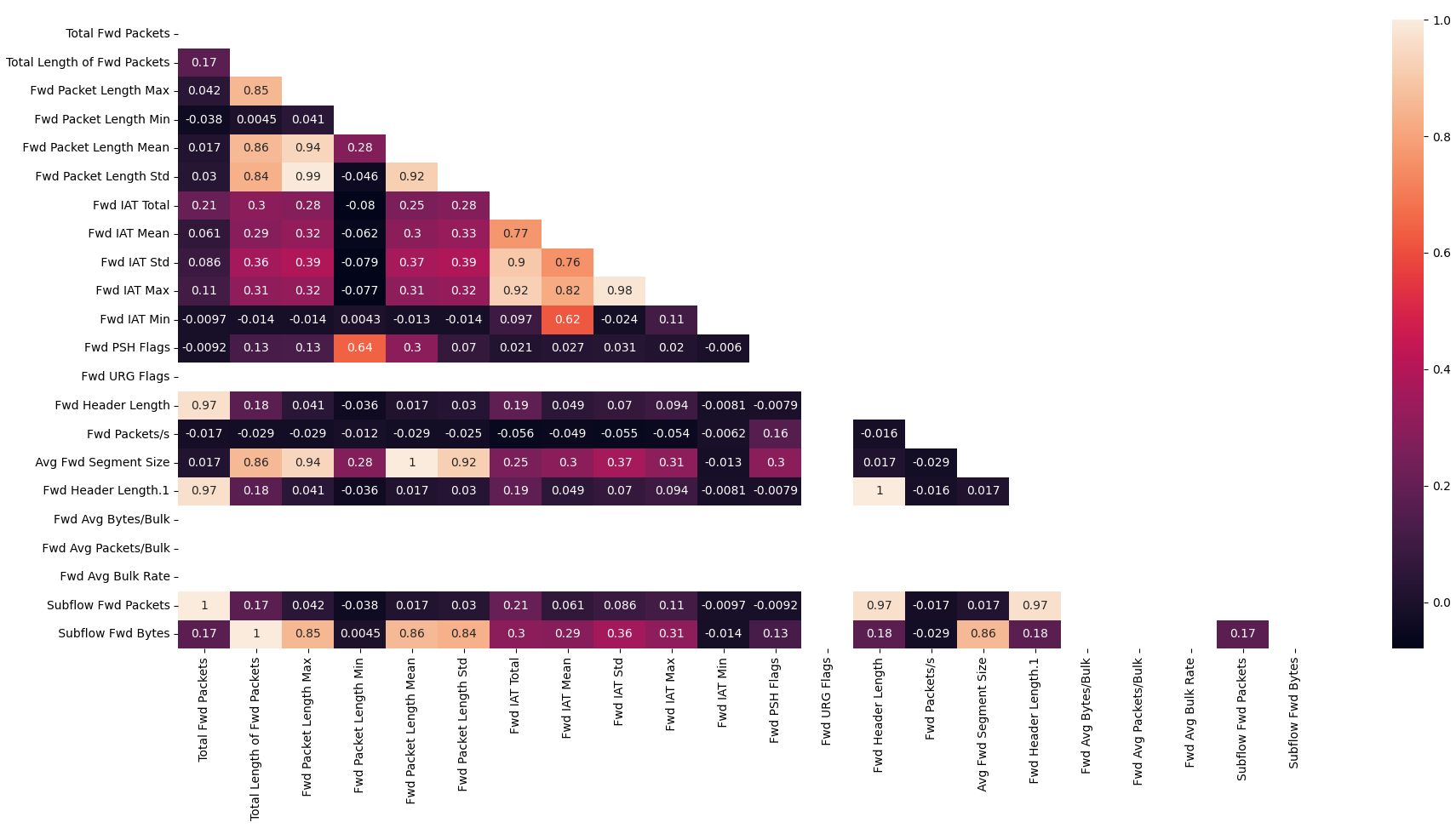
각 특성에 대한 상관관계도를 출력한다. Fig. 5
num_cols = df.select_dtypes(exclude=['object']).columns
fwd_cols = [col for col in num_cols if 'Fwd' in col]
bwd_cols = [col for col in num_cols if 'Bwd' in col]
def getCorrelatedFeatures(corr):
correlatedFeatures = set()
for i in range(len(corr.columns)):
for j in range(i):
if (abs(corr.iloc[i, j])) > 0.95:
print(corr.columns[i],corr.iloc[i,j])
correlatedFeatures.add(corr.columns[i])
return correlatedFeatures
corr = df[fwd_cols].corr()
mask = np.triu(np.ones_like(corr, dtype=np.bool_))
plt.subplots(figsize=(20,20))
sns.heatmap(corr, annot=True, mask=mask)
plt.show()
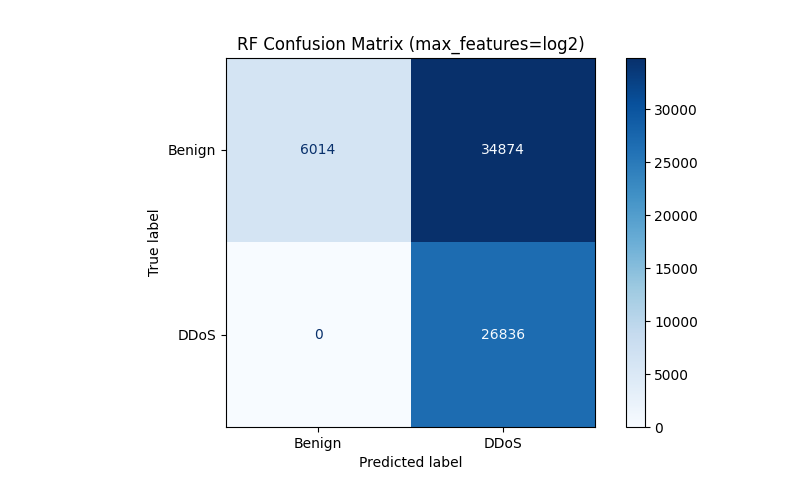
GNB 모델을 학습시킨 후 모델의 종합 결과와 Confusion Matrix 결과를 출력한다. Fig. 6, Table. 1, Table. 2
gnb = GaussianNB() # Gaussian NBC
gnb_fit = gnb.fit(X_train, y_train) # Train model
y_pred = gnb_fit.predict(X_test) # Test and Score
cm=confusion_matrix(y_test, y_pred) # Confusion Matrix
print(cm)
print(classification_report(y_test, y_pred))
print("Accuracy: ", accuracy_score(y_test, y_pred))
disp = ConfusionMatrixDisplay(confusion_matrix=cm,display_labels=["Benign","DDoS"])
disp.plot(cmap='Blues')
plt.title('RF Confusion Matrix')
plt.show()
2.4 시행 결과 평가 #1
2.4.1 첫 번째 시행 결과
첫 번재 시행 결과는 Table. 1, Table. 2과 같다.

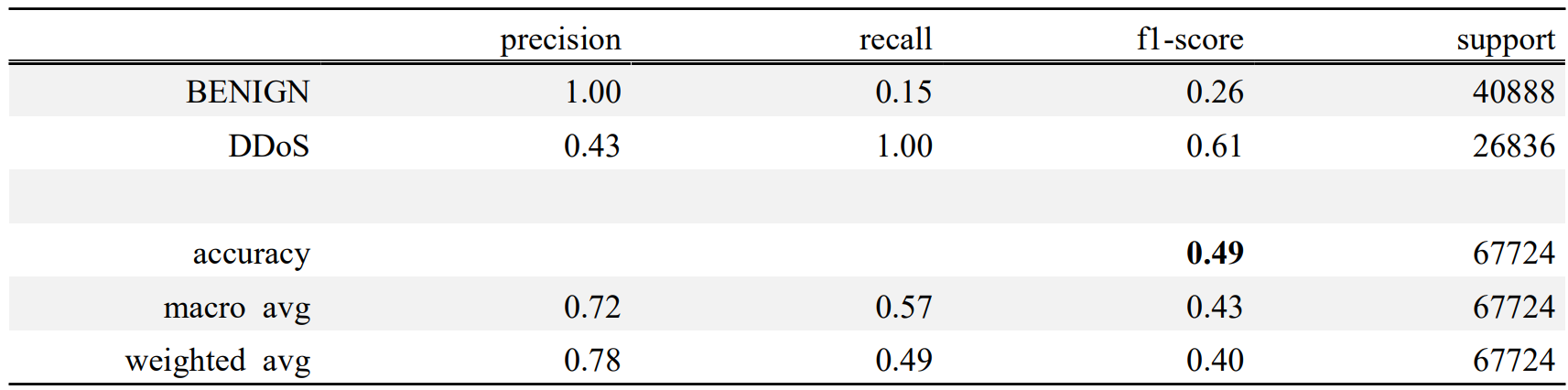
BENIGN은 정상 접근, DDoS는 비정상 접근(공격)을 의미한다. Table. 1에서 빗금 처리된 부분이 이 모델이 제대로 예측한 수를 의미한다(i.e. T를 T로, F를 F로 제대로 예측한 수). 첫 번째 시행에서의 정확도는 약 0.49, 즉 49%로 측정되었다. 본래 예상한 값은 70% 이상이었으나 이를 훨씬 하회하는 결과를 보여준다. 이런 낮은 정확도는 학습과 예측이 올바르게 이루어지지 않았다는 것을 의미한다. 낮은 정확도를 개선하려면 시행 결과를 해석할 줄 알아야 한다.
2.4.2 혼동 행렬(Confusion Matrix)
Table. 1을 해석하려면 혼동행렬(Confusion Matrix)에 대해 알아야 한다. 혼동행렬(i.e. 정오분류표)이란 분류 모델의 성능을 평가하는 지표 중 하나이다.
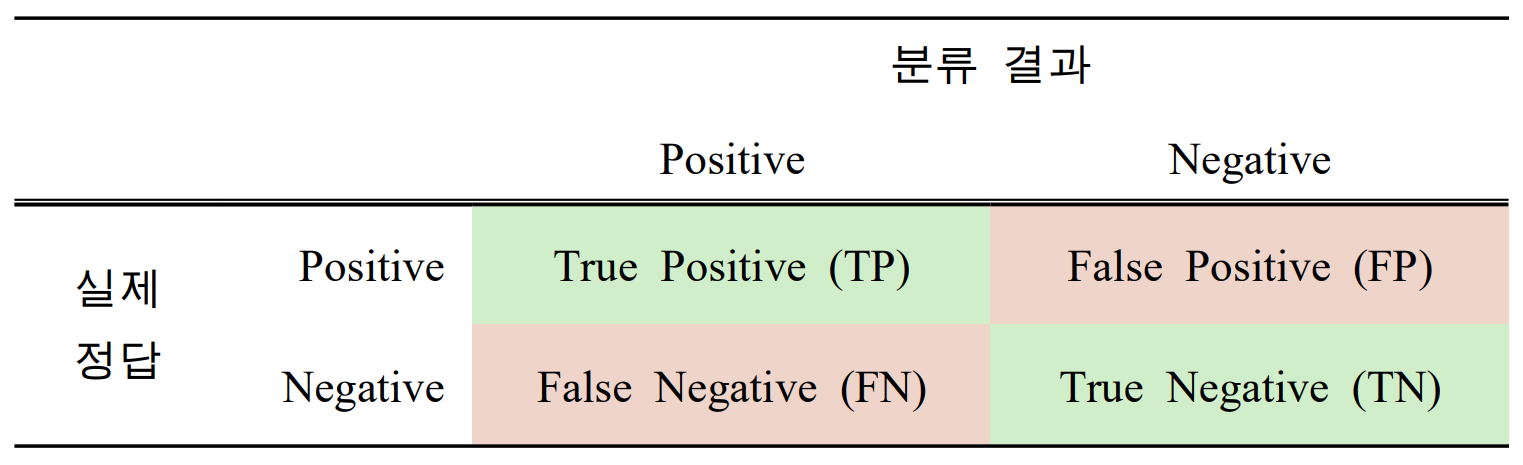
TP와 TN은 정답, FP, FN은 오답을 의미한다. Confusion Matrix를 통해 얻을 수 있는 지표는 재현율(Recall), 특이도(Specificity), 정밀도(Precision), 음성예측도(Negative Predictive Value, NPV)이다.
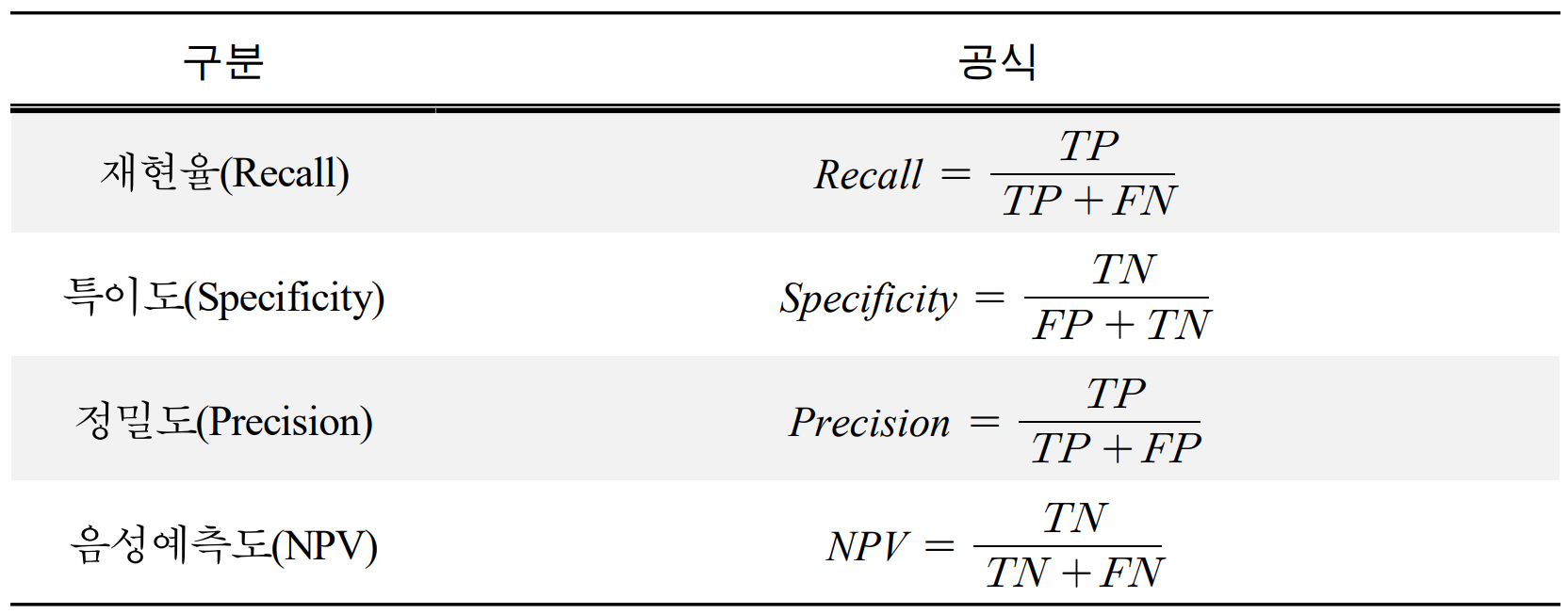
2.4.3 첫 번째 시행의 문제 진단과 개선
보통 FN과 FP는 적절한 비율로 분배되어야 한다. 하지만 Table. 1을 보았을 때 FN이 0인 모습을 확인할 수 있다. 이는 분류 과정이 올바르지 못했다는 의미이다. 이를 해결하기 위해 학습 데이터의 비율에 대한 정확도의 통계를 분석하기로 했다. 이 코드는 i를 변수로 학습 데이터의 양을 0.01부터 0.98까지 조절하였을 때 정확도가 어떤 양상을 보이는지 확인해주는 코드이다. Fig. 7, App. 4
from sklearn import datasets
from sklearn.naive_bayes import GaussianNB
import seaborn as sns
import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
from imblearn.over_sampling import SMOTE
from sklearn.metrics import confusion_matrix, classification_report, f1_score, precision_score, recall_score, accuracy_score,ConfusionMatrixDisplay, roc_curve
from sklearn.model_selection import train_test_split
# module import endline #
x1 = []
y1 = []
data=pd.read_csv('./dataset.csv',chunksize=100000,index_col=0) # import dataset(csv)
df = pd.concat(data)
for i in range(1, 99):
x=df[[' Flow Duration',' Total Fwd Packets', ' Total Backward Packets',,' Idle Min']]
y=df[' Label']
X_train, X_test, y_train, y_test = train_test_split(x, y, train_size=i/100, shuffle=False, random_state=1004)
gnb = GaussianNB() # Gaussian NBC
gnb_fit = gnb.fit(X_train, y_train) # Train model
y_pred = gnb_fit.predict(X_test) # Test and Score
x1.insert(i, i/100)
y1.insert(i, accuracy_score(y_test, y_pred))
print(i, " Accuracy: ", accuracy_score(y_test, y_pred))
plt.plot(x1, y1)
plt.xlabel("train_size")
plt.ylabel("accuracy")
plt.show()
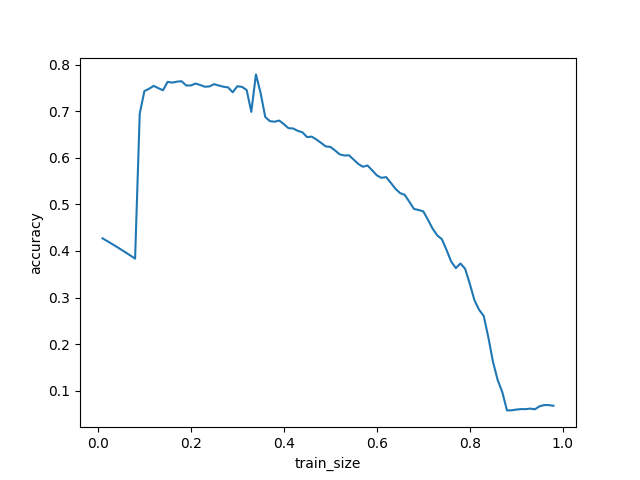
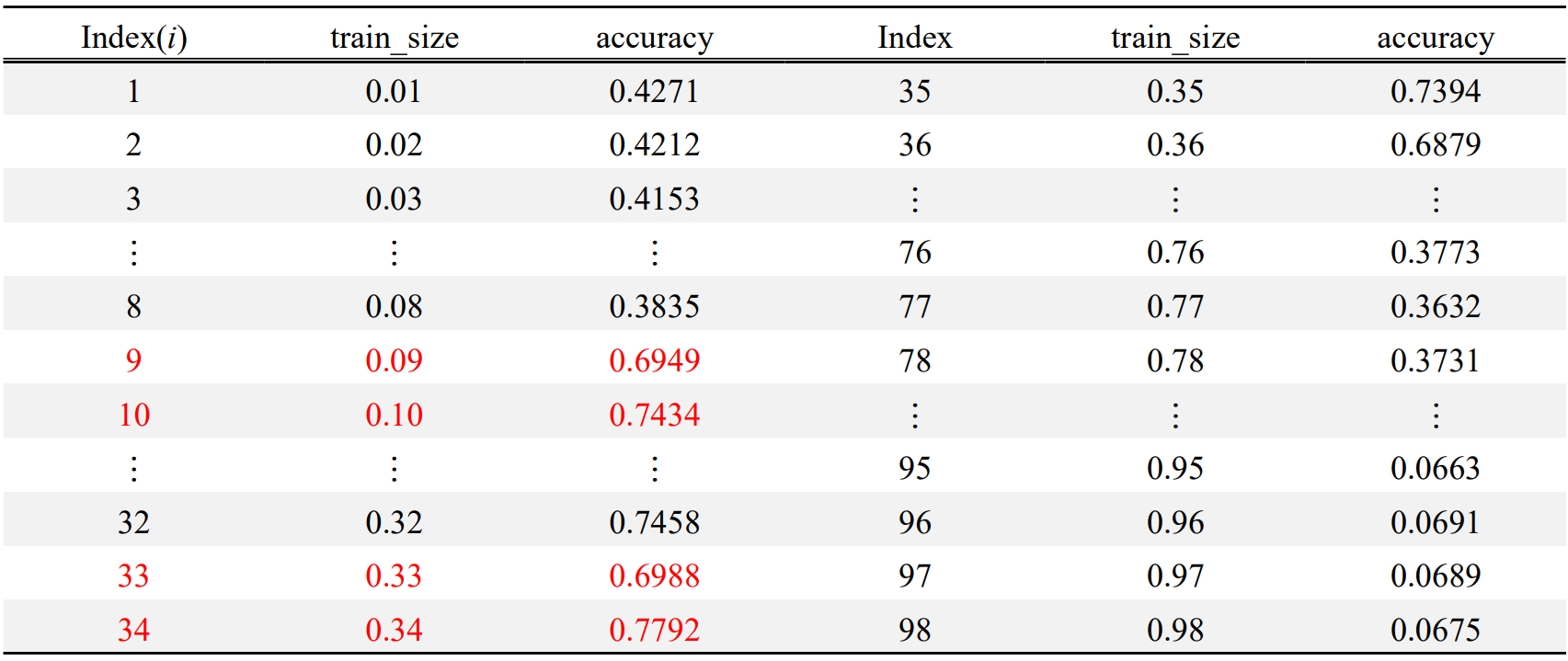
Fig. 7과 Table. 5를 교차대조하였을 때, 9번과 10번, 33번과 34번에서 값이 튀는 것을 볼 수 있다. 이런 튀는 값들을 이상치로 분류하였을 때, 정확도의 최댓값은 18번에서의 0.7646이다. 따라서, train_size를 0.18로 하였을 때 가장 높은 정확도가 나올 것이라 생각할 수 있다.
2.5 시행 결과 평가 #2
2.5.1 두 번째 시행 결과
두 번째 시행 결과는 Fig. 8, Table. 6, Table. 7과 같다.
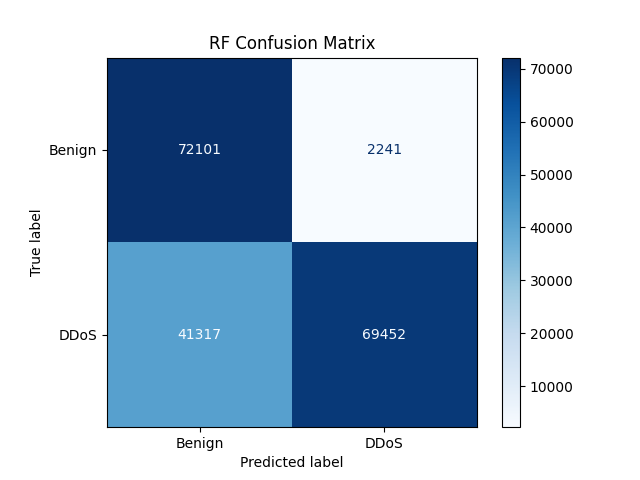

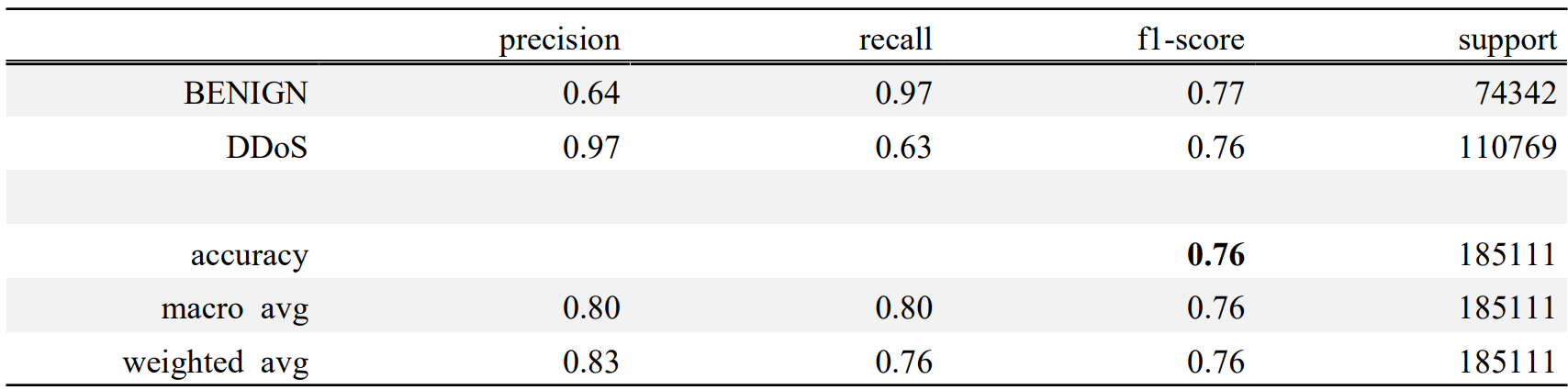
두 번째 시행에선 정확도가 0.76으로 측정되었다. 테스트 데이터의 양이 늘었으므로, 전체적인 혼동행렬의 절대적인 수치도 증가하였다. 첫 번째 시행과 다른 점이라면 두 번째 시행에서는 첫 번째 시행에서보다는 FN와 FP가 어느정도 분배되었다. 아직 편향성이 보이긴 하나 이는 데이터셋의 근본적 한계로 생각된다.
3. 결론
3.1 마치며
이번 연구를 통해 나이브 베이즈를 비롯한 다양한 분류 알고리즘을 알게 되었다. 파이썬을 이용해 직접 AI를 학습시키면서 알 수 없는 오류가 발생하는 등 여러 난관이 있었지만 꾸준한 노력과 주변에 코드를 잘 다루는 분들께 자문을 구해 해결할 수 있었다. 이 자리를 빌려 감사의 말씀을 드린다.
또한 데이터 마이닝에 대해 더욱 심층적으로 알 수 있게 되었다. 인터넷에 떠도는 학술 자료를 찾아보며 알지 못했던 새로운 내용이나 알고 있었지만 부족하게 알고 있었던 것, 심지어 잘못 이해하고 있던 내용을 고치고, 숙지할 수 있게 되었다. 한편 이 내용은 대학교 컴퓨터공학부에서 배우는 내용이니만큼 이 보고서에선 다소 생략된 내용이 있거나 논리의 비약이 있을 수 있다. 하지만 스스로 이론을 최대한 숙지하려 노력하였다.
한편 이 실험이 2017년부터 프로그래밍을 시작하면서 여태 진행한 실험 중 가장 난이도가 높았다고 체감했다. 아무래도 고등학교 3학년 과정의 확률과 통계가 엮여있고, 직접 AI를 만드는 것이 난이도가 높은 것이 이 실험을 어렵게 만든 원인인 것 같다. 직접 AI를 만들어 보면서 AI 연구자, 개발자들의 고충과 무엇이 의미있는 데이터인지, 무엇이 이상치인지, 상관관계를 어떻게 보는지 등을 알게 되어 어려웠지만 큰 의미가 있었다고 생각한다. 단순히 생활기록부 기재만을 위해 이해도 안 되는 어려운 지식을 단순히 복사해 긁어오는 것 보다는 말이다. 이 보고서는 실제로 내가 여러 연구와 독서를 통해 직접 얻은 지식들로 구성했다. 이해가 안 되는 것들은 이해하려 노력했고, 주변에 코딩을 잘 다루는 분들에게 자문을 받기도 했다. 이런 일련의 학습 활동이 내게는 의미있게 다가왔고, 앞으로도 시간이 남는다면 이런 활동을 자주 해볼 예정이다.
3.2 참고사항
- 본 보고서는 서면으로 제공되거나, PDF로 제공됩니다. 또한 개인 운영 블로그인 https://blog.ardan.kr/에도 기고됩니다. App. 5의 QR코드를 통해 접속할 수 있습니다.
- 프로젝트 파일은 블로그에서 다운로드 가능합니다. App. 5의 QR코드를 통해 접속할 수 있습니다.
- 본 보고서에서 사용된 모든 이미지의 저작권은 본 보고서의 저자에게 귀속됩니다.
- 모든 사진, 자료, 논문을 포함한 저작물의 저작권은 해당 저작자에게 귀속됩니다.
- 본 보고서는 생활기록부 기재용으로써, 생활기록부 기재 이외의 다른 역할을 하지 않습니다.
- 본 보고서는 크리에이티브 커먼즈 라이선스(CCL)를 따릅니다. CC BY NC ND.
참고 문헌
Sebastian, R., & Yuxi, H. L., & Vahid, M. (2023). Machine Learning with PyTorch and Scikit-Learn. (박해선 번역).
구본권. (2022). ‘정보 홍수’에서 가장 중요한 능력은? 월드와이드웹: https://enterprise.kt.com/bt/dxstory/985.do에서 2024. 1. 8.에 검색함.
기획재정부 시사경제용어사전. (2020). 무어의 법칙(Moore's Law). 월드와이드웹: https://www.moef.go.kr/sisa/dictionary/detail?idx=1073에서 2024. 1. 10.에 검색함.
G. E. Moore, (1965, April). Cramming More Components onto Integrated Circuits. 83–84.
Lee, Sang-Gi, Lee, Byeong-Seop, Bak, Byeong-Yong, & Hwang, Hyekyong. (2010). A Study of Intelligent Recommendation System based on Naïve Bayes Text Classification and Collaborative Filtering. Journal of Information Management, 41(4), 227–249. https://doi.org/10.1633/JIM.2010.41.4.227
Bayes, Thomas, Richard Price. (1763). An Essay towards solving a Problem in the Doctrine of Chances. By the late Rev. Mr. Bayes, F. R. S. communicated by Mr. Price, in a letter to John Canton, A. M. F. R. S. (PDF). 《Philosophical Transactions of the Royal Society of London》 (영어) 53: 370–418.
I. Sharafaldin, A. H. Lashkari, S. Hakak and A. A. Ghorbani, "Developing Realistic Distributed Denial of Service (DDoS) Attack Dataset and Taxonomy," 2019 International Carnahan Conference on Security Technology (ICCST), Chennai, India, 2019, pp. 1-8, doi: 10.1109/CCST.2019.8888419.
